对法线变换矩阵的理解

tangent向量($T$)表示和surface平行的向量，在三角形中可以用两个vertex的差计算，
所以T的变换矩阵和vertex的一样，但法线($N$)不同，由于有切变的存在，如果还用相同的矩阵左乘，变换之后的法线将不再和原来的surface垂直:

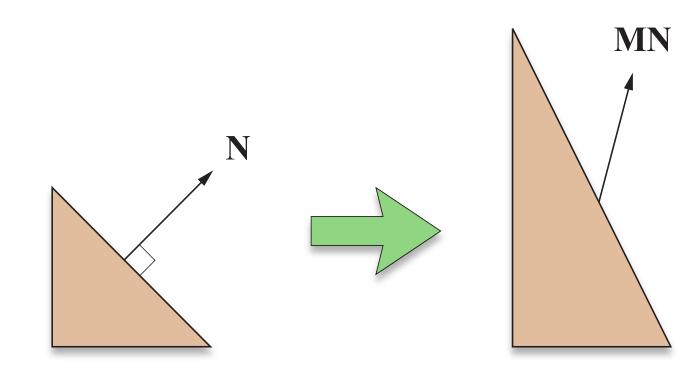
为了确保变换之后的法线依然垂直于surface, 可以从如下条件出发进行推导:
$$
N\cdot T=N^{\prime}\cdot T^{\prime}=0
$$

推导过程：

最终有：
$$
G=\left( M^{-1} \right) ^T
$$

即法线的变换矩阵是原矩阵的逆转置(inverse transpose)

如果原矩阵是正交矩阵，那么有：
$$
M^{-1}=M^T
$$
代入上式可得：
$$
G=M
$$
也就是说如果原来是正交变换，那么法线可以直接用原来的矩阵变换

其实几何上是因为，正交矩阵行向量与列向量皆为正交的单位向量，所代表的变换只能是旋转或镜像，有保证原始图形不变形的特性，叫做保距映射，那么因为原来的图形没有变形，法线自然也就不用特殊处理