齐次坐标与变换的几何解释

代数理解

对于为何引入齐次坐标，一般的分析文章都会从代数的角度出发，给出如下公式：
$$
\left[ \begin{array}{c}
x\\
y\\
z\\
1\\
\end{array} \right] \left[ \begin{array}{ccc:c}
a_{11}& a_{13}& a_{13}& t_x\\
a_{21}& a_{22}& a_{23}& t_y\\
a_{31}& a_{32}& a_{33}& t_z\\
\hdashline
0& 0& 0& 1\\
\end{array} \right] =\left[ \begin{matrix}
M& T\\
0& 1\\
\end{matrix} \right] \left[ \begin{array}{c}
P\\
1\\
\end{array} \right] =\left[ \begin{array}{c}
MP+T\\
1\\
\end{array} \right]
$$

从式中可以看出，构造特殊的4维矩阵，就可以让计算之后的结果，正好是原来向量与左上角的3维矩阵相乘(MP)，再加上偏移变换T

没毛病，但是如果能从几何的角度去解释这个事情，就可以更透彻的理解变换矩阵

二维情况

一个二维的点$(x, y)$, 加上第三个维度并赋值1，变为 $(x, y, 1)$, 其几何本质是把原来二维$xoy$平面上的点，看做三维空间中$z=1$的平面上的点在$xoy$平面的投影：

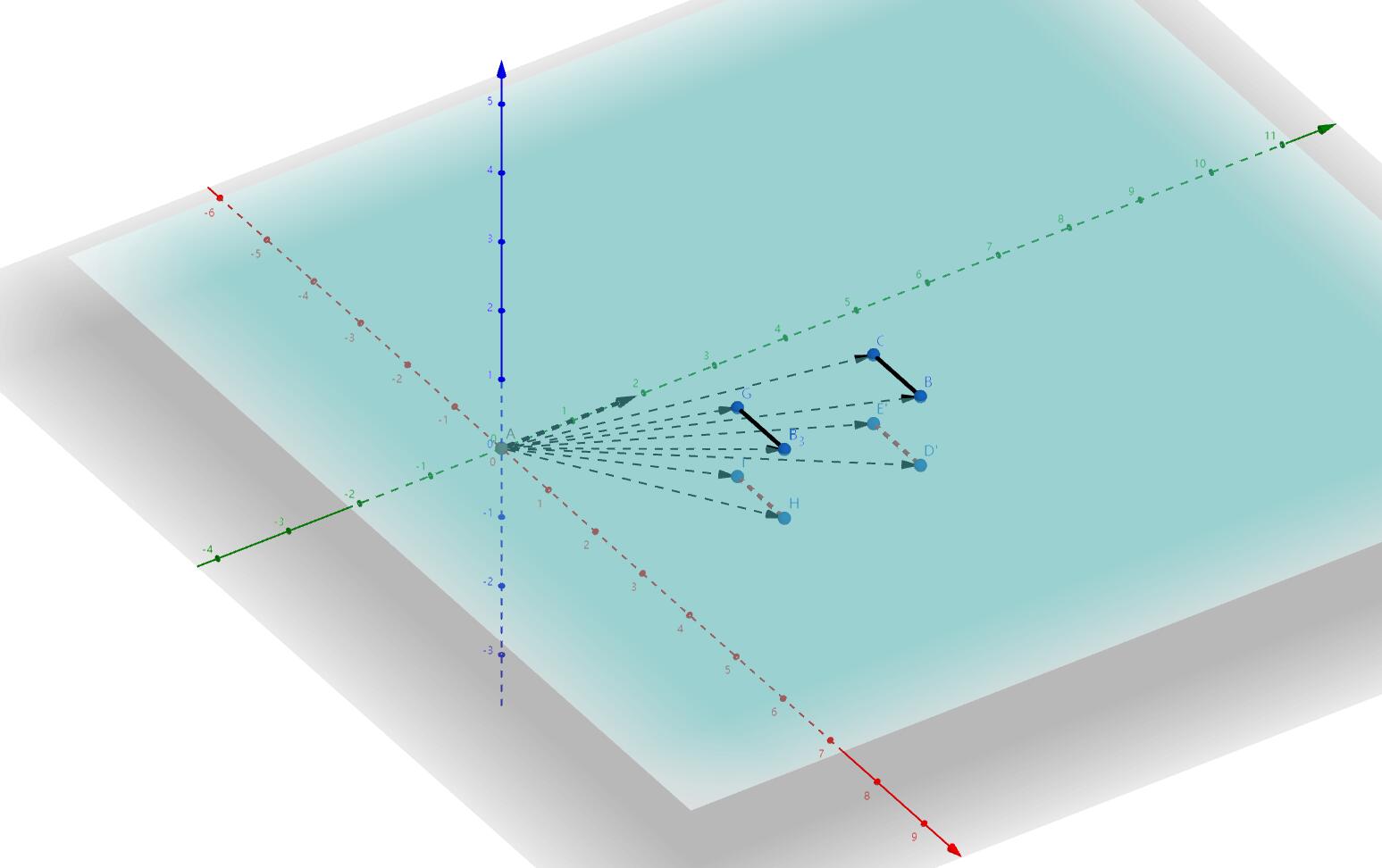
如果把二维齐次坐标看作普通的三维向量，那么平移矩阵:
$$
\left[ \begin{matrix}
1& 0& t_x\\
0& 1& t_y\\
0& 0& 1\\
\end{matrix} \right]
$$
其实表示的是三维空间中的一个切变，切变之后的物体投影到二维$xoy$平面，正好就是二维空间中的平移变换:

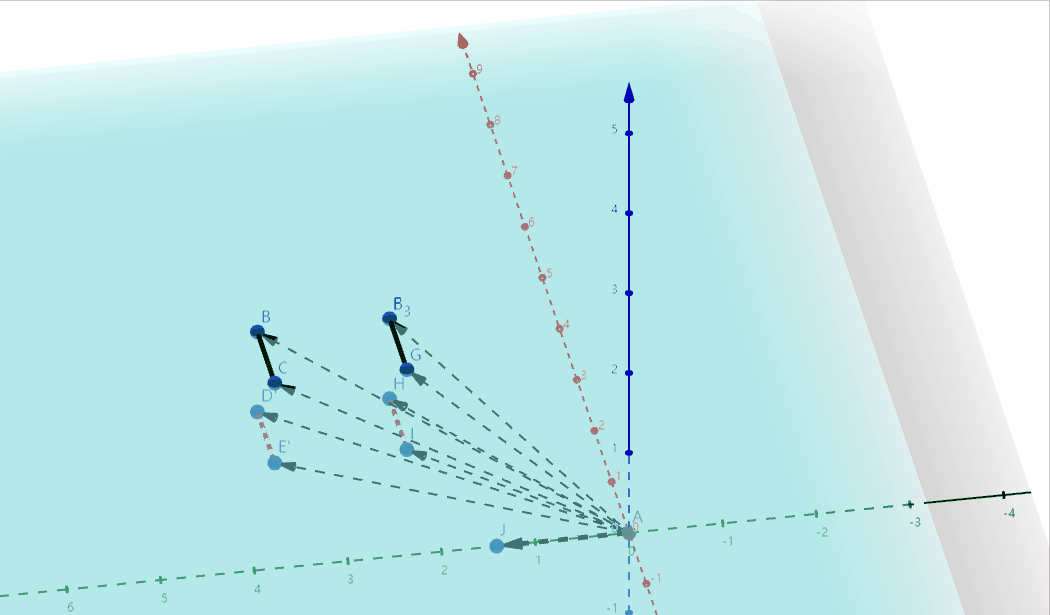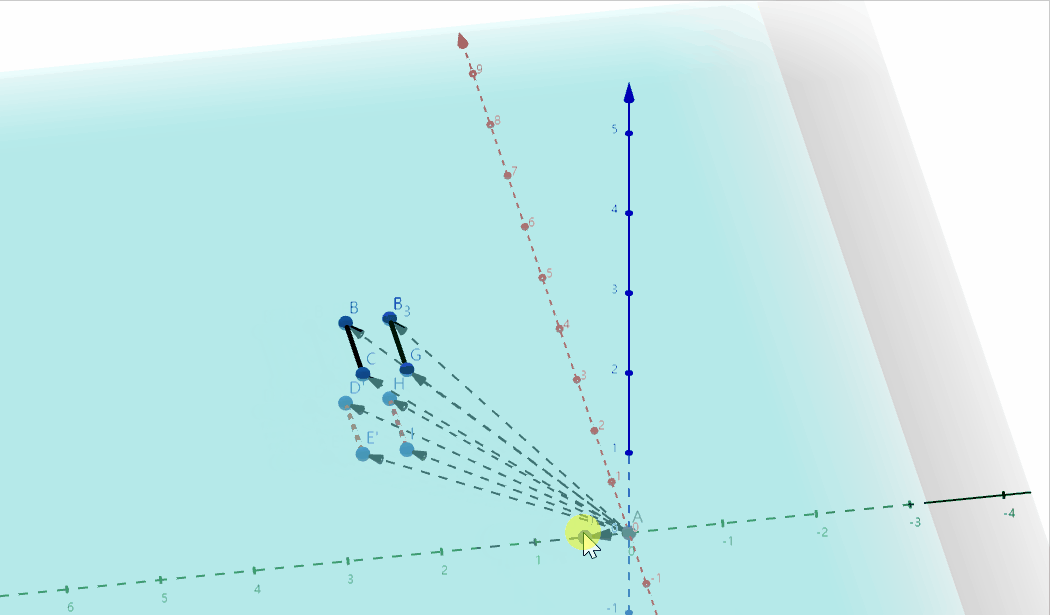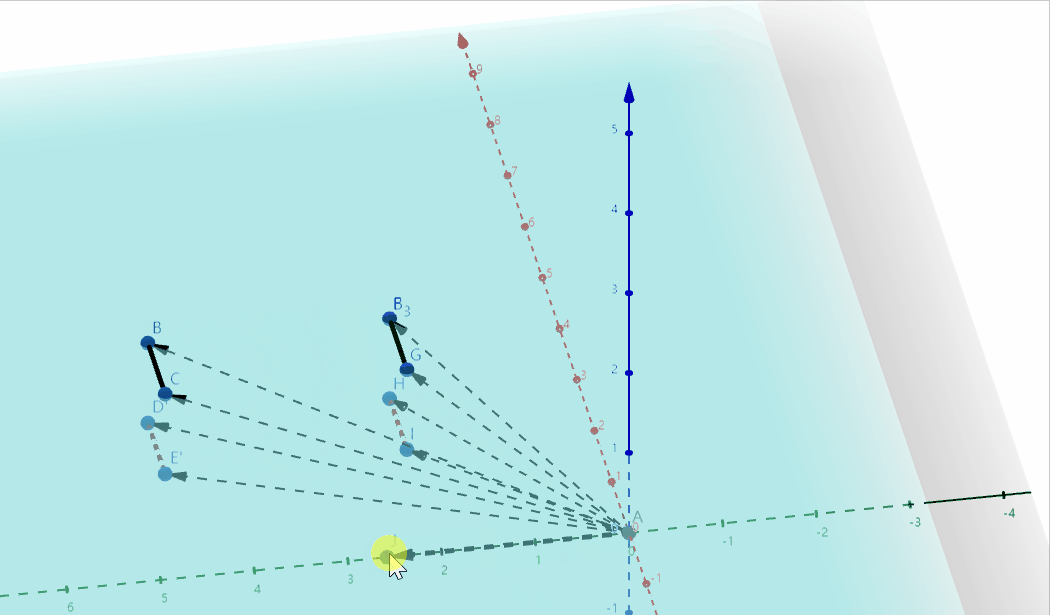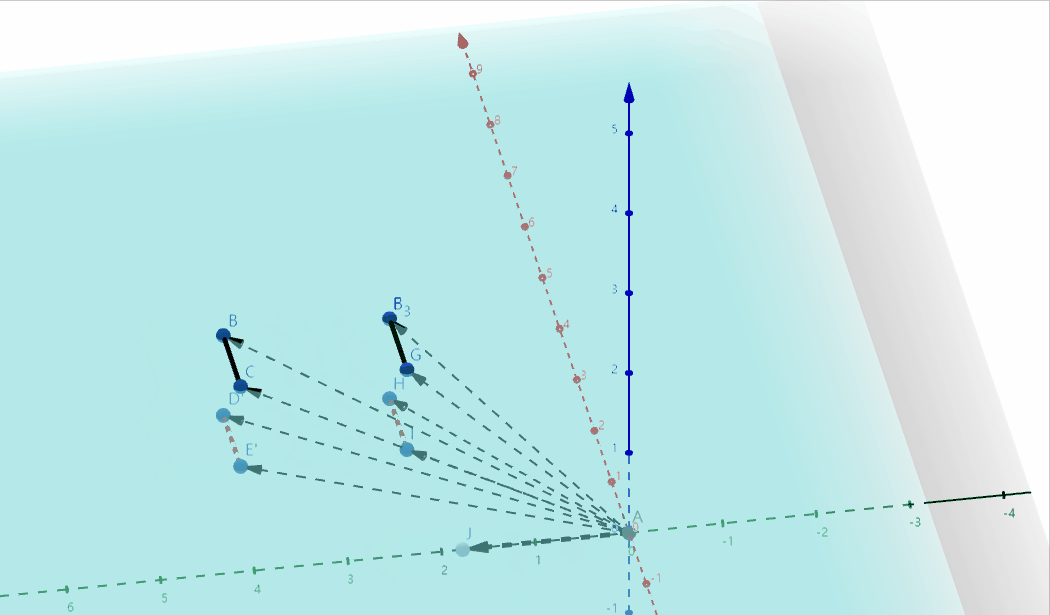
我们知道，矩阵只能用来表示线性变换，而线性变换只有缩放、旋转、切变三种，所以不升维的情况下，同维的矩阵无法表示平移变换
通过提升一个维度，把高维的切变投影成低维的平移，就很好的解决了这个问题

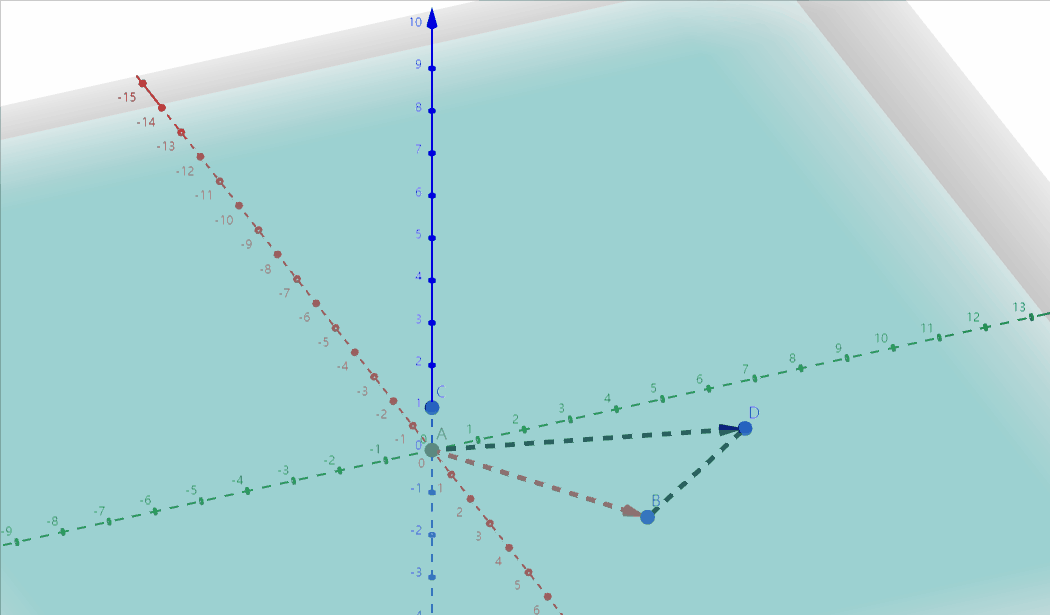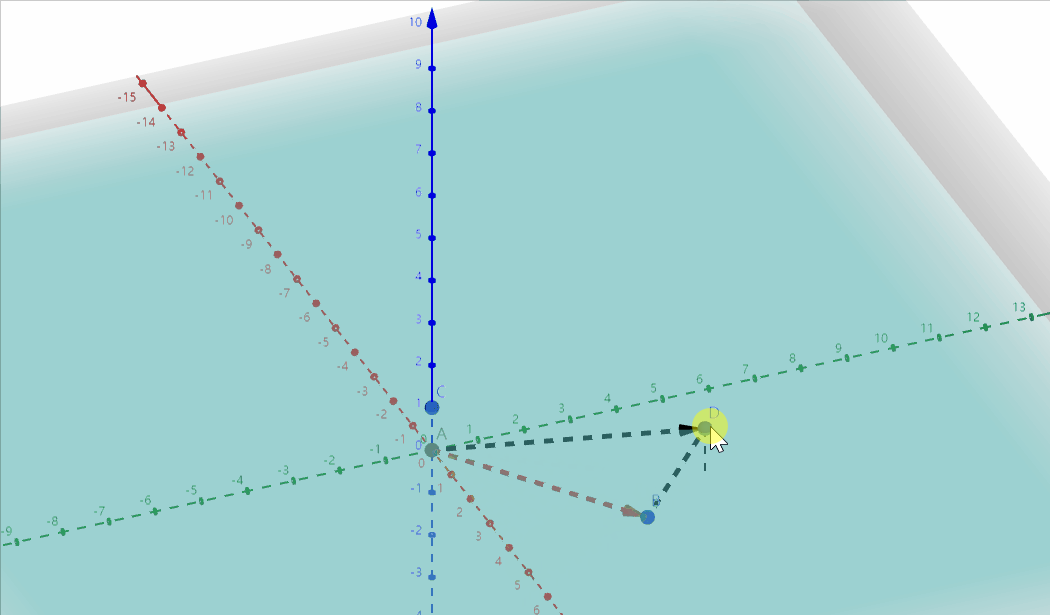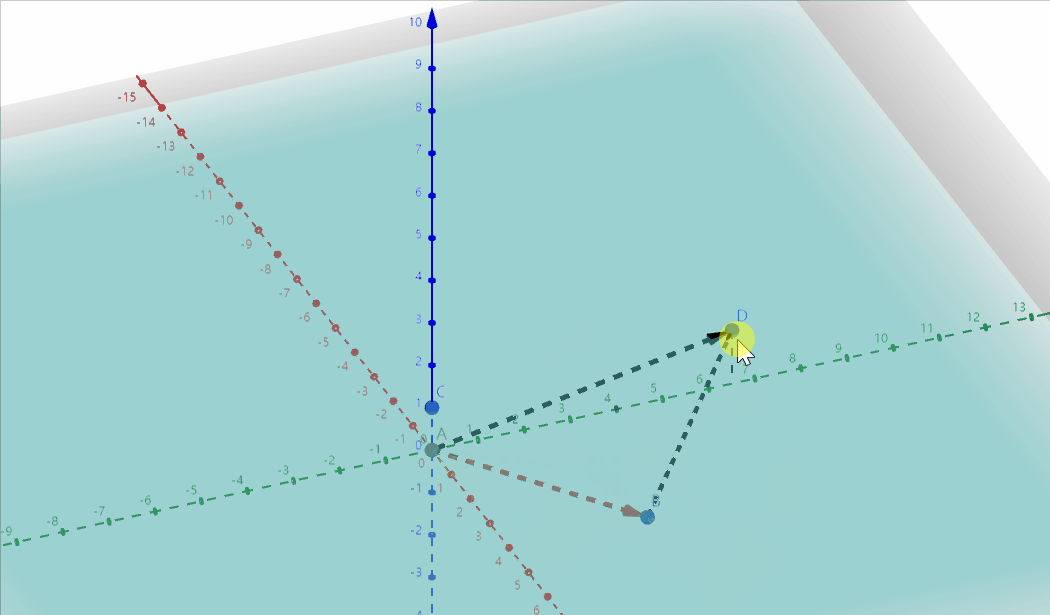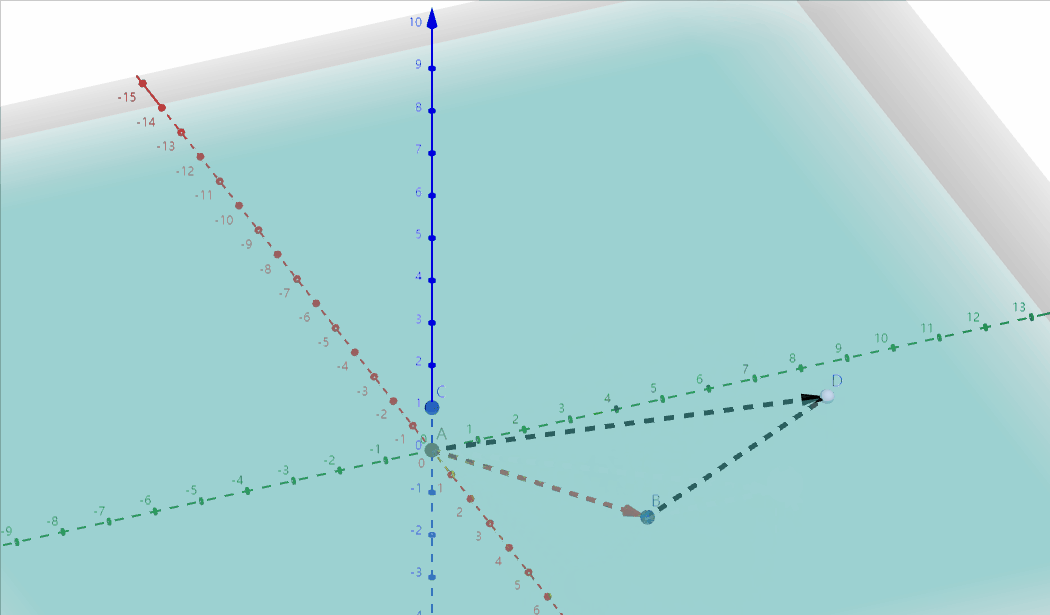
这也解释了另一个问题，就是$w$元素为什么为1时表示点，为0时表示方向：
因为切变操作会固定一个平面 ($z=0$平面), 平移另一个平面 ($z=1$平面)，如果点在移动的平面上(对应$w=1$)，就会被移动，投影也会跟着移动，而点在静止平面上(对应$w=0$)，就不会被移动，而方向向量恰好就是不会被移动的，如图：

此外，如果不升维的话，要表示平移变换，就只能 $MP+T$, 连续两次变换就是 $M_2(M_1P+T_1) + T_2$,三次以上就更麻烦
而使用高维齐次矩阵，连续的变换就可以仅用一次矩阵相乘解决，简洁高效

三维情况

到了三维，情况其实也是一样的，只不过由原来三维投影到二维，变成了四维投影到三维，而四维平移矩阵表示的也是四维空间中的一个切变

这里有个难点，就是我们可能不容易想象出四维空间中的切变的几何形状是什么样的，毕竟我们都是三维生物
要想清楚这一块其实也不难，首先我们得能在脑中构造出一个四维立方体

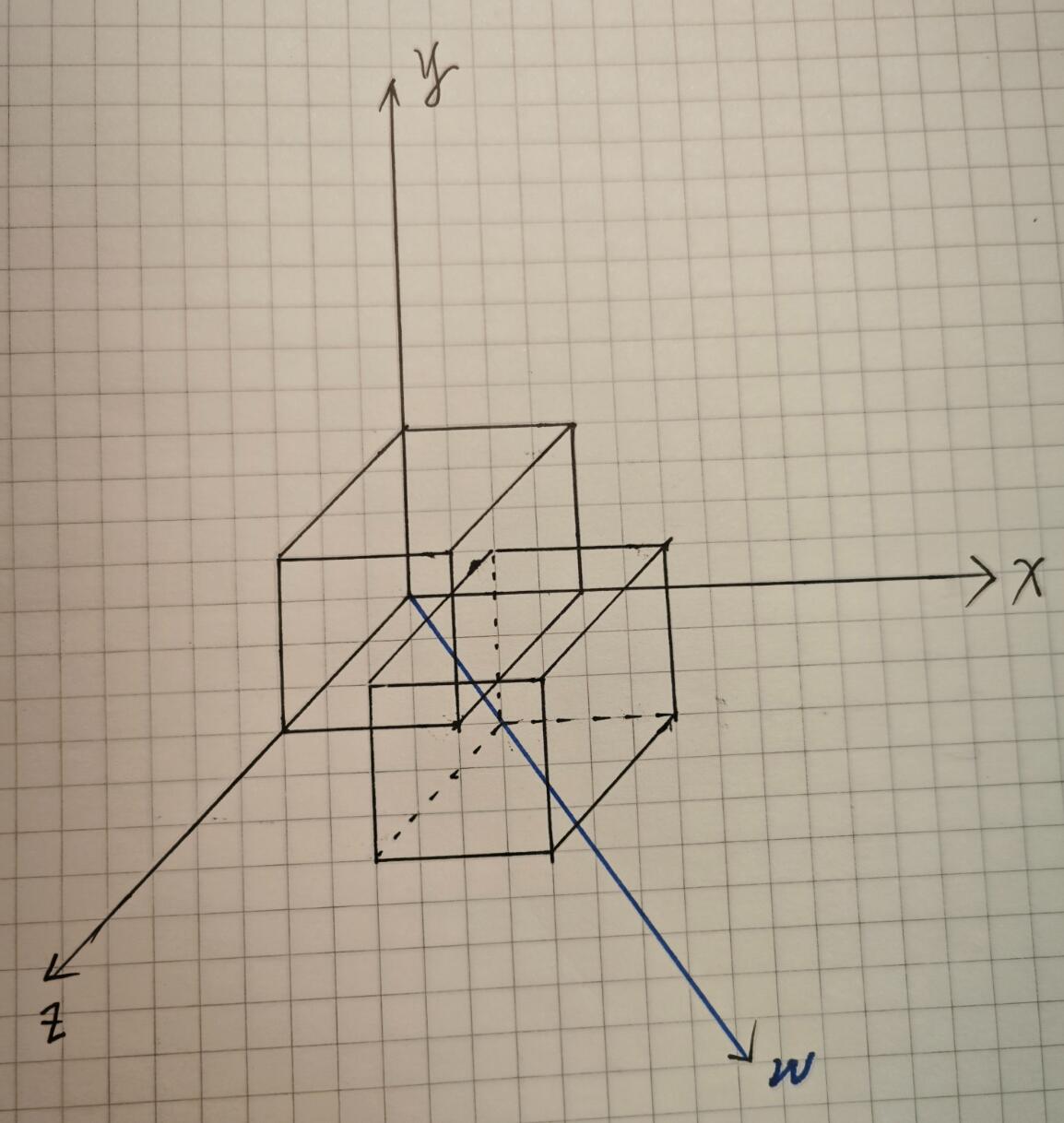
设第四个坐标轴为$w$轴，直接想比较困难，我们可以先画出$w$轴不垂直于其它三轴的情形，然后再推到垂直的情况，就容易了：
先画出平移前后的两个胞体：

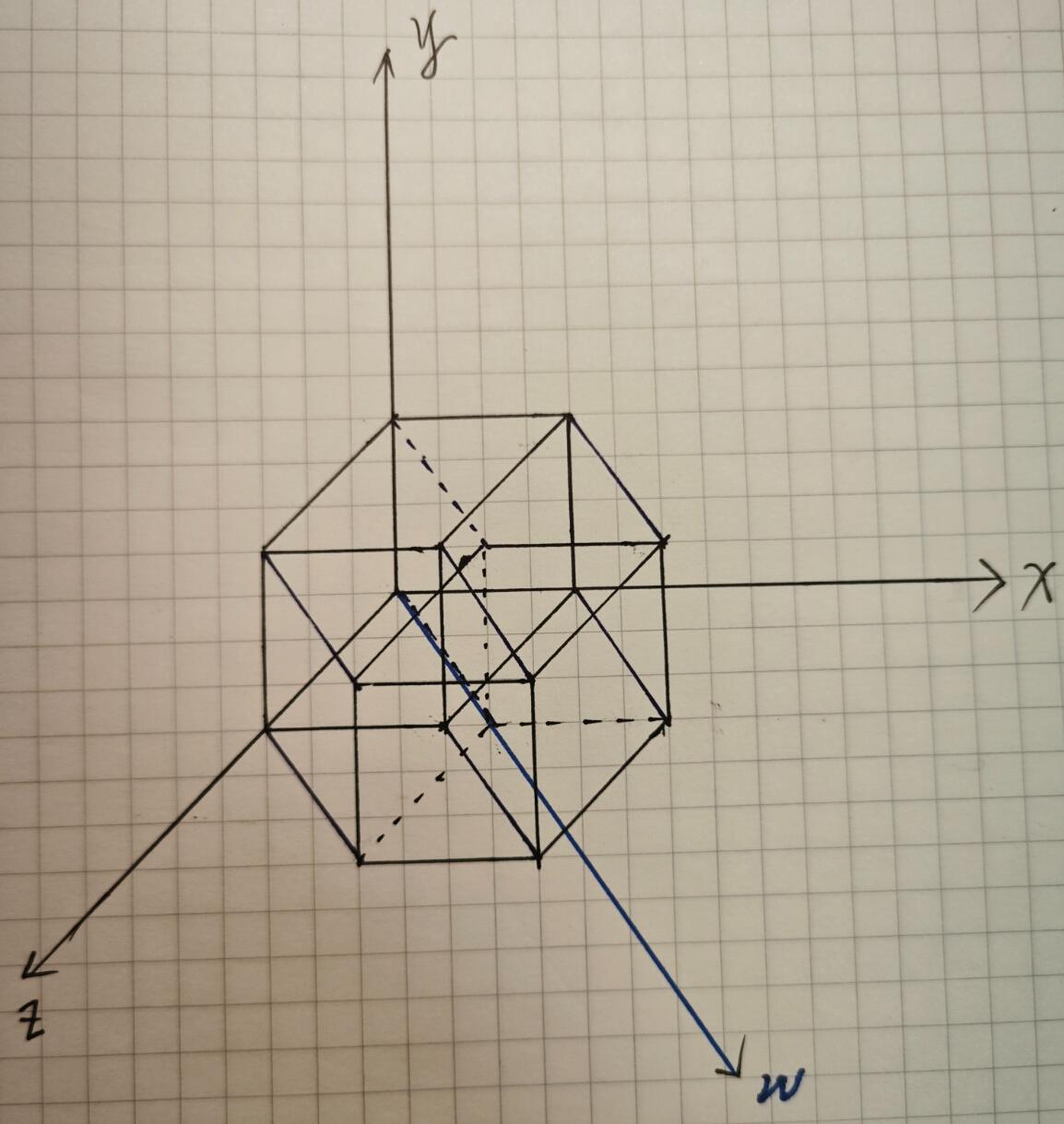
再把8个顶点依次连线，就得了一个四维立方体的二维投影：

我画的是不垂直的情况，网上找了张垂直的：

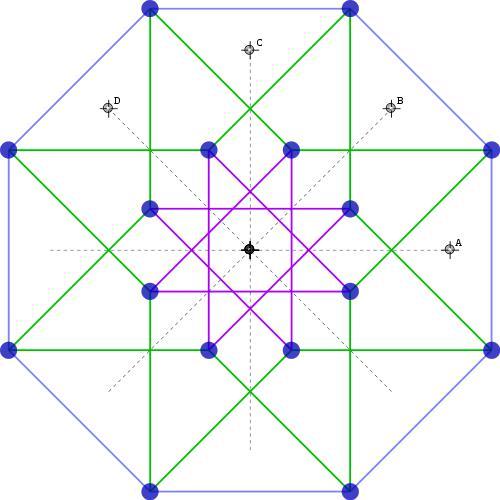
观察这个投影，可以看到一个四维立方体有8个胞体，移动前后本身有两个，六个面各形成一个，加起来8个
类比三维中$z=1$平面上的切变，四维空间中的切变，其实就是在$w=1$的子空间上的切变，切变之后再投影到三维，就变成了平移