Path Tracing 中 Russian Roulette 的期望

简介

Path Tracing 的递归算法中要解决一个问题，就是光线不能无限反射，需要有一个停止的条件，一种方法就是使用俄罗斯轮盘赌，Russian Roulette (RR)，只有通过RR时才继续算反射，否则停止递归，这样即能避免无限递归，又能保证能量守恒。

误区

和群友Irimsky `讨论发现之前自己的计算是不对的，之前我认为期望就简单这么算：
$$
E\left( p \right) =1p+2p^2+3p^3+\cdots +np^p
$$
就简单反射次数乘以$p$的$n$次方，最后算出来：
$$
E\left( p \right) =\frac{p}{\left( 1-p \right) ^2}
$$
但是这是不对的，这种情况下$p=0.5$，期望是2次，$p=0.8$，是20次。
为此我还写了段代码来数值计算：

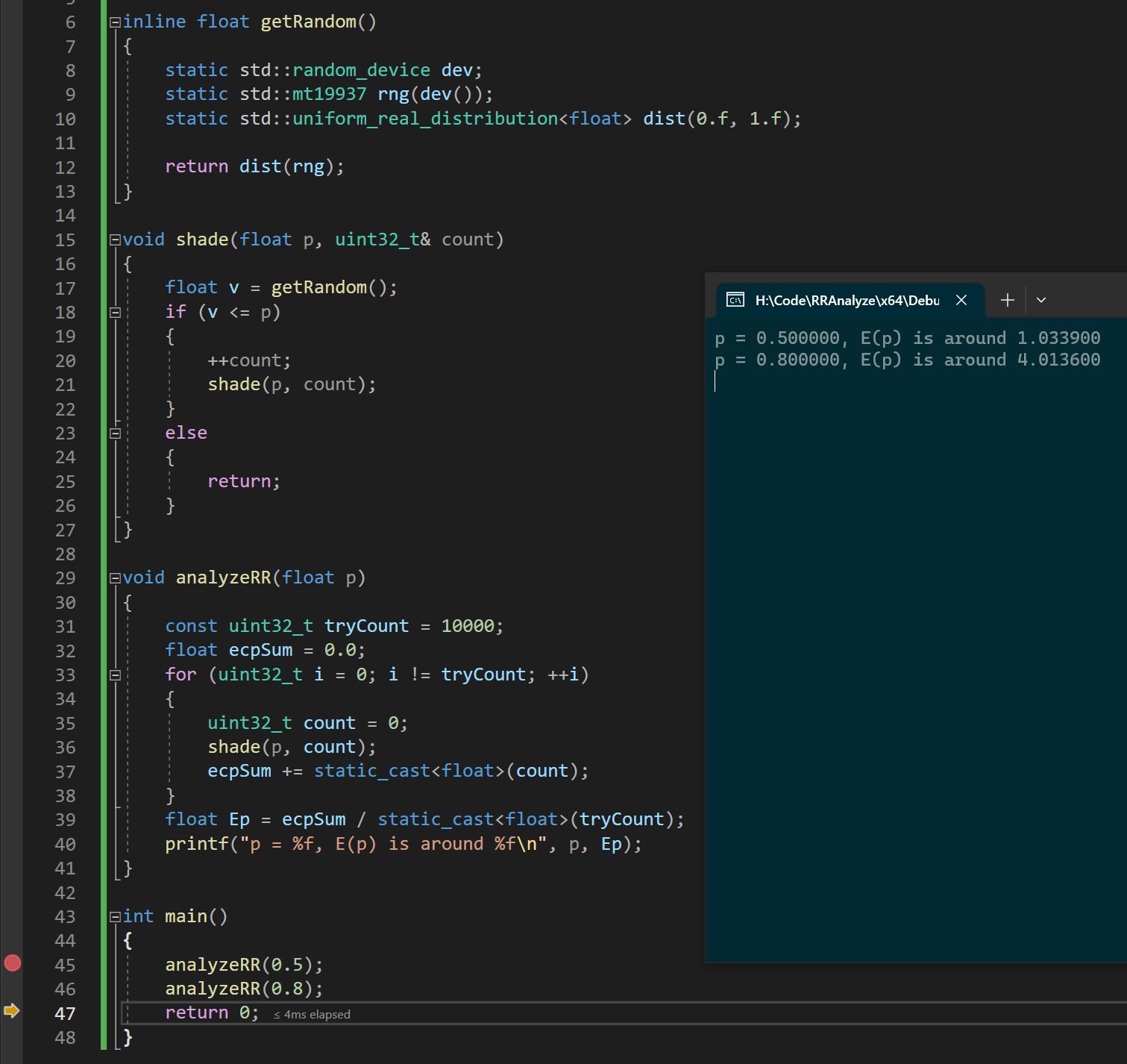
结果显然和上面的公式不符，那么错到哪了呢？ 错的地方就在于，之前计算的时候，没有考虑失败的情况，比如说认为反射2次的情况是$2p^2$，但是这种情况下，**第3次会不会反射是不确定的**，正确的算法应该是再乘以失败的概率来终结反射，也就是$3p^2(1-p)$

结论

设RR通过概率概率是$p$，$p=0$不反射，$p=1$无限次反射，$0<p<1$时期望为：
$$
E\left( p \right) =\frac{p}{1-p}
$$

也就是说，如果$p=0.5$，那么大体上会反射2次，$p=0.8$，大体上会反射4次


其实这里的概率就是几何分布，几何分布就是求前n-1次失败的前提下，第n次成功的概率，如果熟悉概率公式，几何分布的期望就是：
$$
E\left( p \right) =\frac{1}{p}
$$
对于我们的情况，要把成功和失败反过来，因为我们要算的是前n-1次成功，第n次失败情况，也就是说，赌局总次数的期望为：
$$
E\left( p \right) =\frac{1}{1-p}
$$
再减去最后一次的失败，那么反射次数就是：
$$
S\left( p \right) =E\left( p \right) -1
\
=\frac{1}{1-p}-1
\
=\frac{p}{1-p}
$$

推导过程

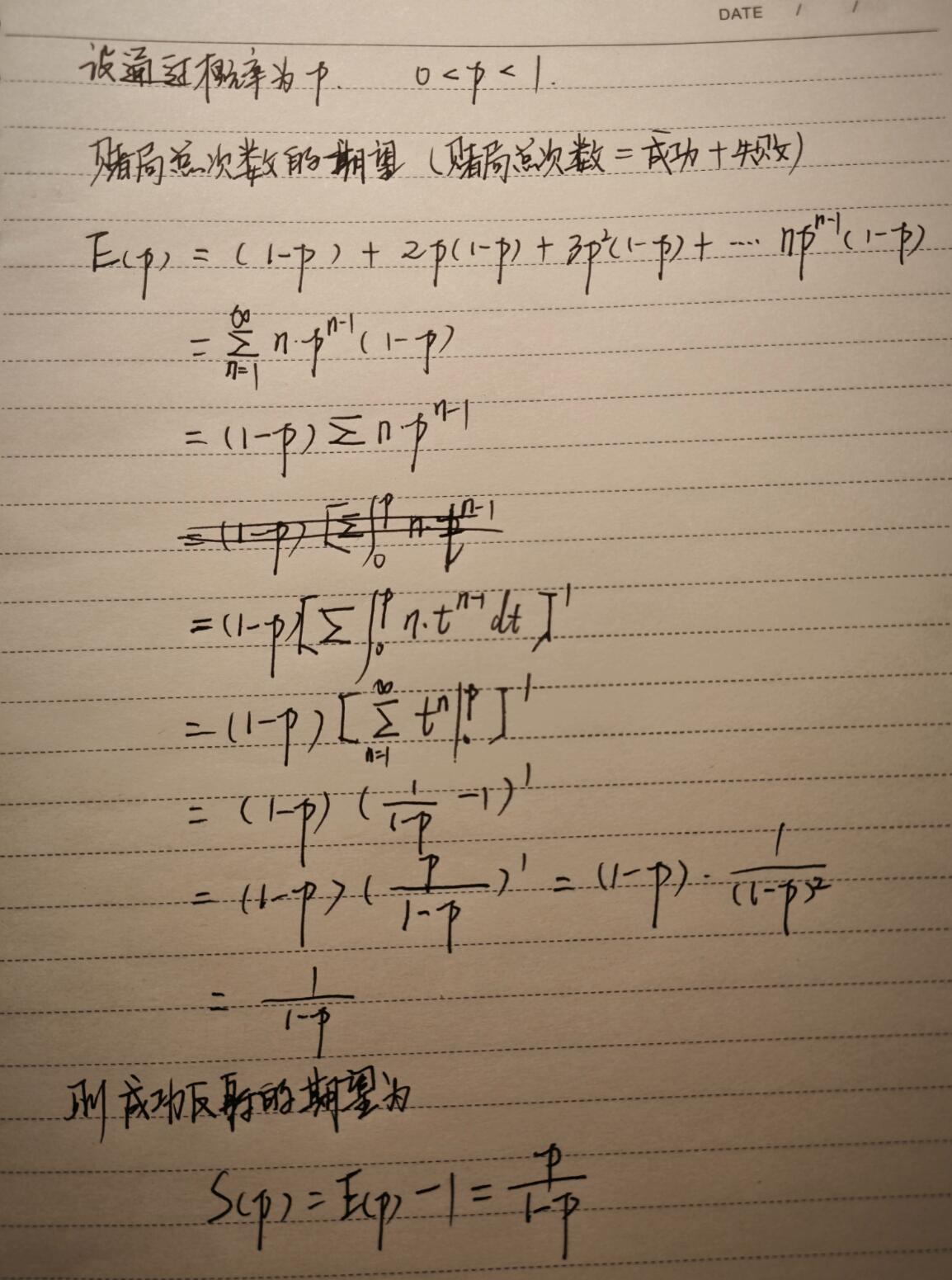
相关资料

Games 101
https://www.bilibili.com/video/BV1X7411F744?t=3248.4&p=16