球谐函数的计算与证明

曲线空间坐标

其实想获得球坐标下拉普拉斯方程，完全可以不用曲线坐标，直接把球坐标的参数方程代入到拉普拉斯方程中一步步求微分，也能算出来，但是这样计算量会非常大，稍微马虎就会出错，而如果拿到曲线坐标下计算，过程要简单的多

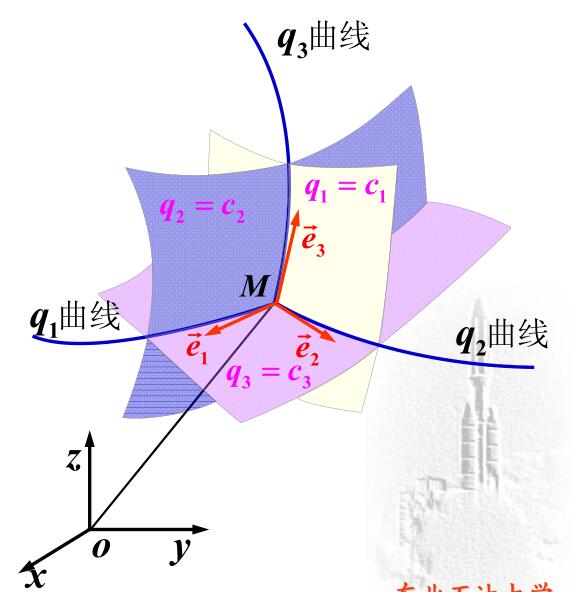
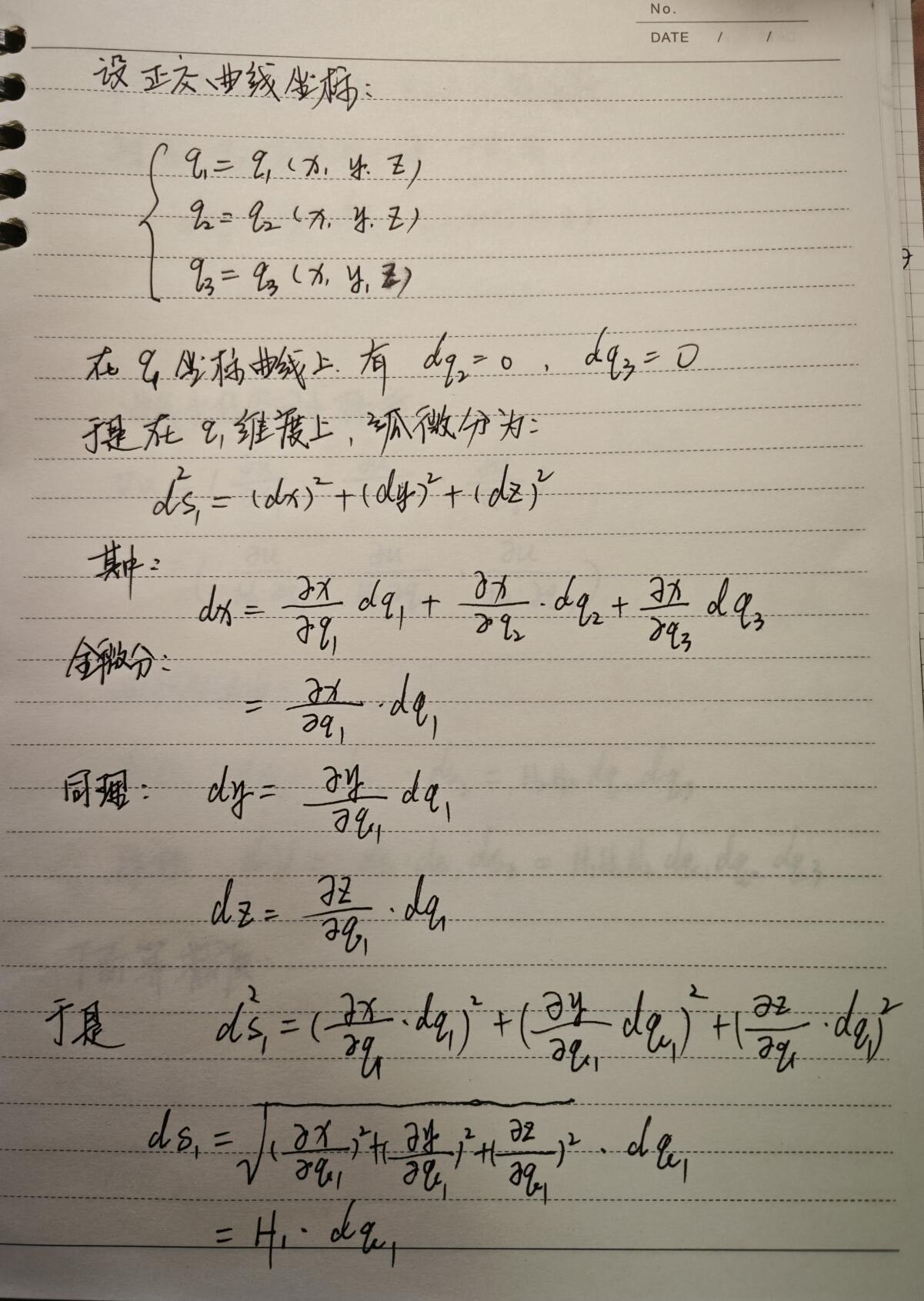
球坐标下拉普拉斯方程

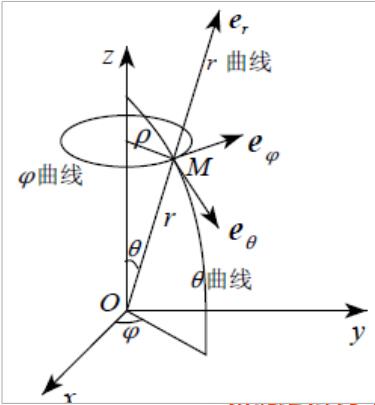
曲线坐标下的坐标值，不一定表示长度，也可以是角度等，比如下面要计算的$\theta ,\varphi $就是角度量，为了转换成直角下的长度，就需要一个比率系数，这就是拉梅系数。

对于$r$分量，在曲线坐标中移动一个单位长度，直角坐标中也是移动一个单位长度，所以$H_r=1$

而$\theta$分量移动一个单位，对应直角坐标中沿球面经向转过$\theta$角度，那么直角坐标中长度的变化量就是$r$，所以$H_{\theta}=r$

最后的计算结果是符合直觉的。

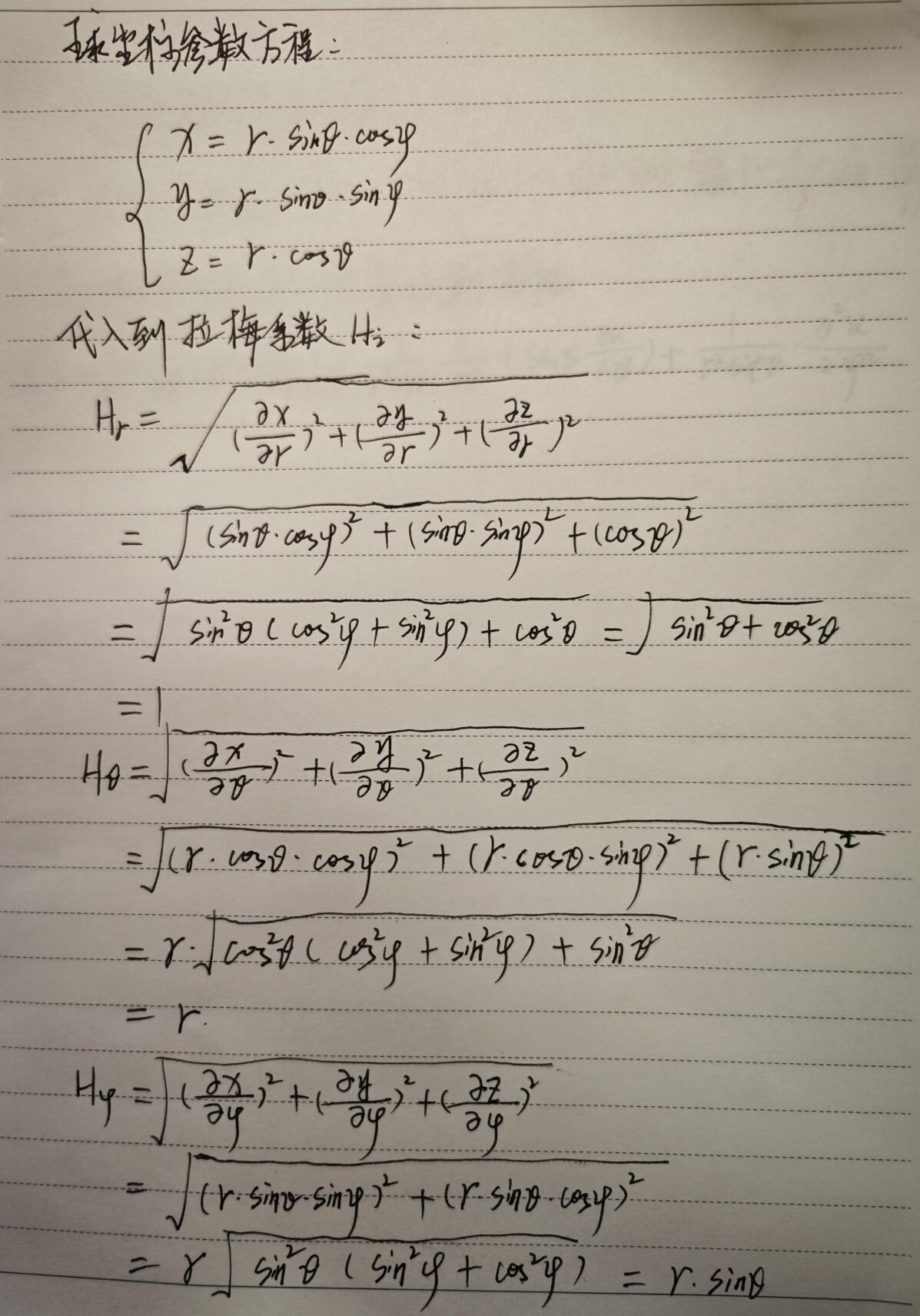
分离变量法

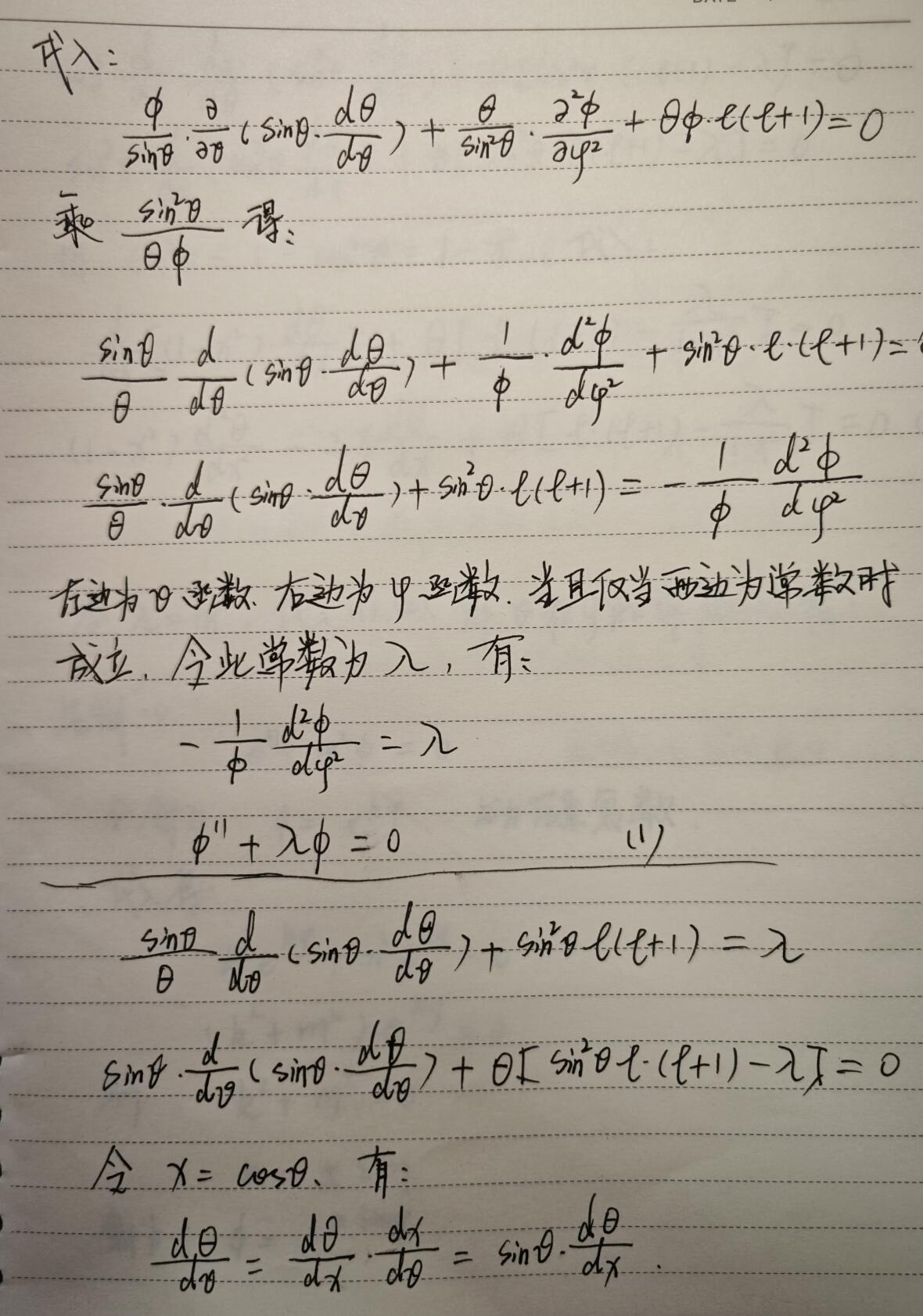
解 $\varphi $ 微分方程

解 $\theta $ 微分方程

解勒让德方程

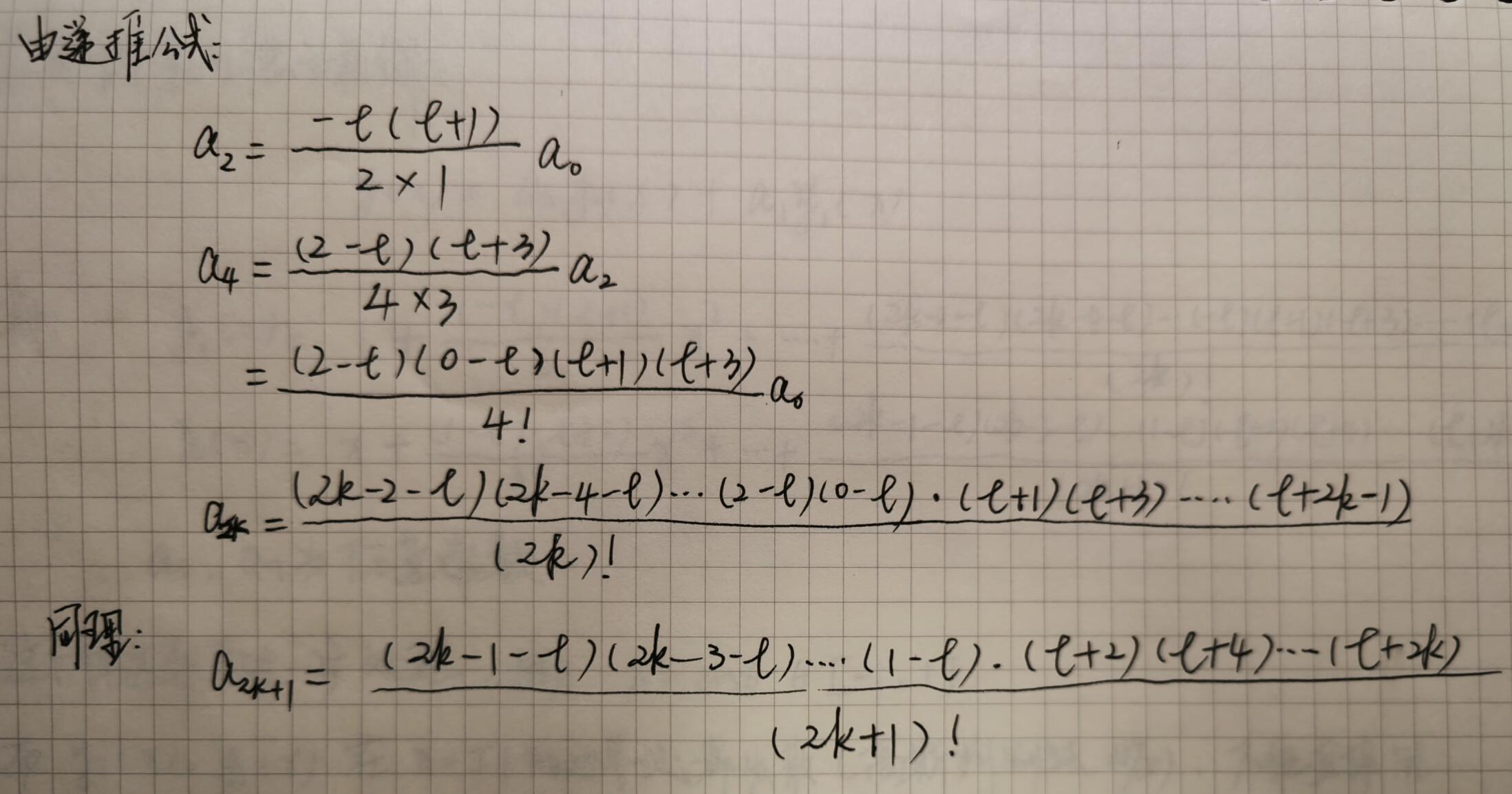
解连带勒让德方程

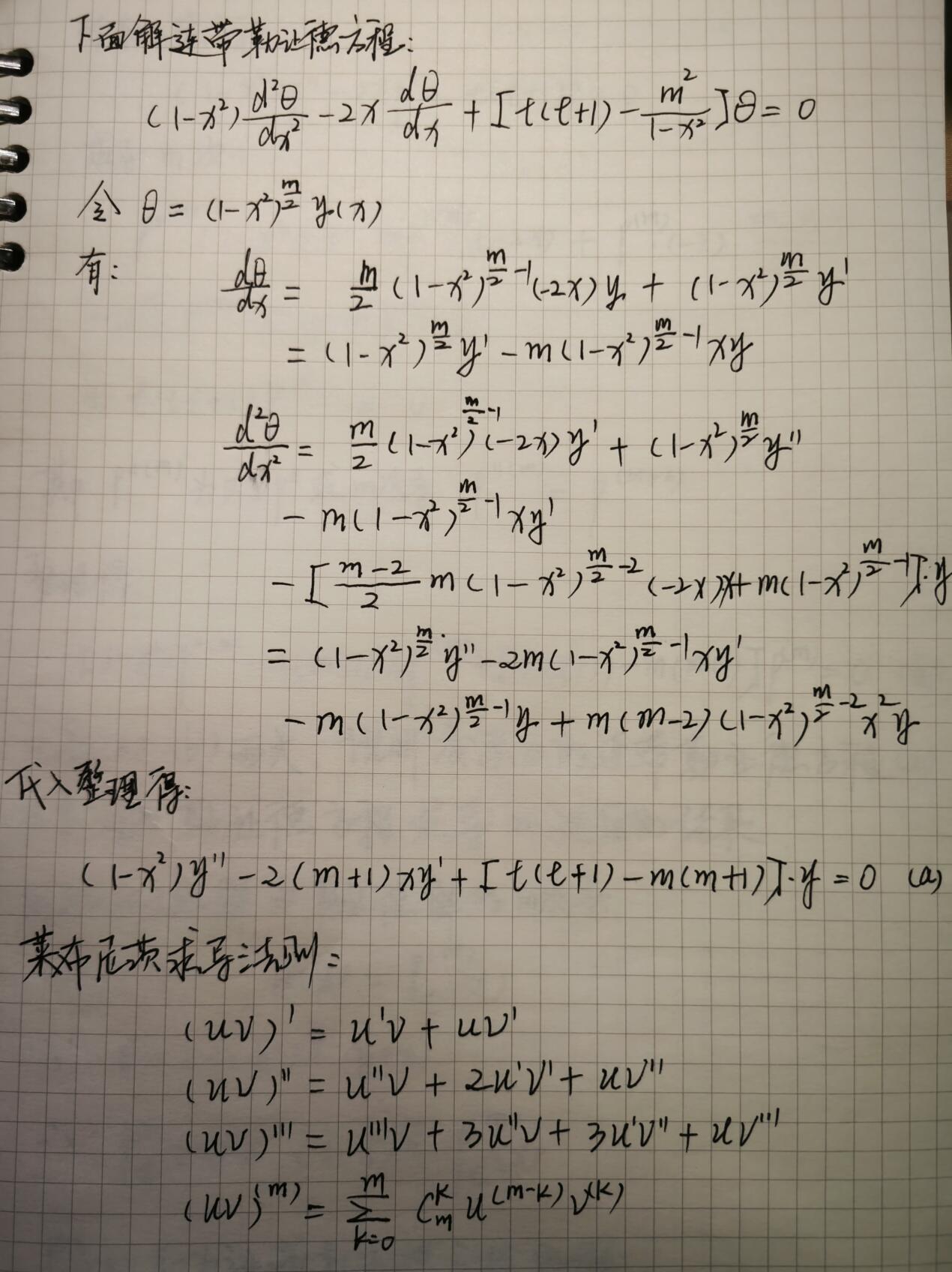
球函数

还得祭出这张图，图中从上到下依次为$l=0, 1, 2, 3$阶球函数，蓝色为正值，黄色为负值，颜色越亮绝对值越大。

另外之所以有像电子云(并不是)一样的形状，只是因为除了颜色以为，图中还使用到原点的距离来表示了$Y_{l}^{m}$函数的值。
可以这样理解，首先在单位球面上取一点$P(x, y, z)$,把点$P$坐标代入球函数$Y_{l}^{m}$，这样会计算出一个值$d$，在原点至$P$点的连线$OP$上截取长度为$d$的线段$OD$，这样取遍单位球上的点$P$，就可以得到所有对应的点$D$, $D$的合集就是图上的奇怪形状了

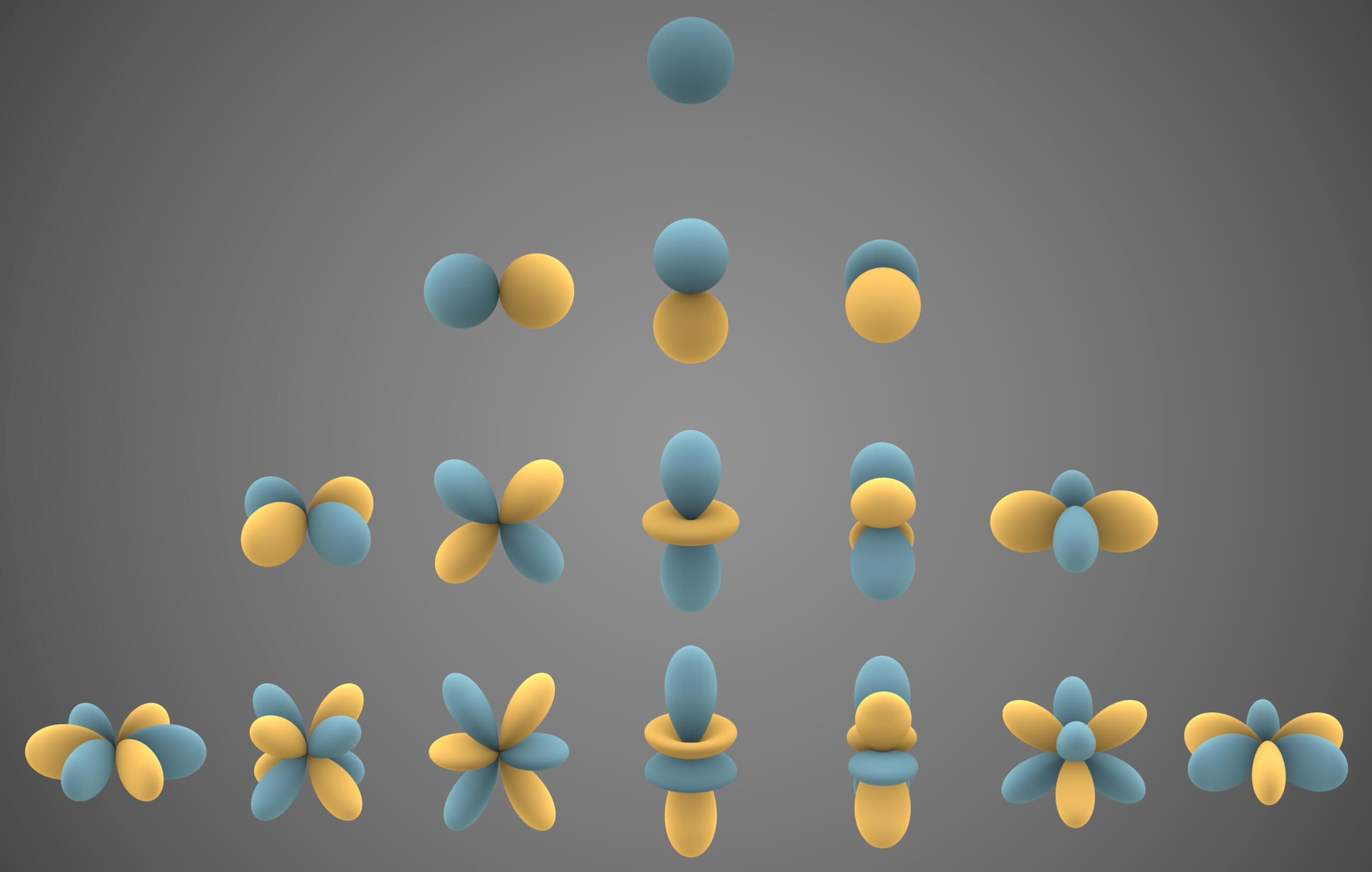
旋转不变性

此即为球函数的加法公式，可以根据球心至球面任意两点连线形成的两向量的内积，不随球坐标旋转而改变，这一性质来证明
TODO

计算举例

可以看到和UE5里SH函数计算结果一致:

template<> 
inline TSHVector<3> TSHVector<3>::SHBasisFunction(const FVector& Vector) 
{
	TSHVector<3> Result;
	Result.V[0] = 0.282095f; 
	Result.V[1] = -0.488603f * (float)Vector.Y;	// LWC_TODO: Precision loss
	Result.V[2] = 0.488603f * (float)Vector.Z;
	Result.V[3] = -0.488603f * (float)Vector.X;

	FVector VectorSquared = Vector * Vector;
	Result.V[4] = 1.092548f * float(Vector.X * Vector.Y);
	Result.V[5] = -1.092548f * float(Vector.Y * Vector.Z);
	Result.V[6] = 0.315392f * float(3.0f * VectorSquared.Z - 1.0f);
	Result.V[7] = -1.092548f * float(Vector.X * Vector.Z);
	Result.V[8] = 0.546274f * float(VectorSquared.X - VectorSquared.Y);
	return Result;
}